I wanted to pay off my student loans in the most efficient way possible. Most people use the "snowball" method, whereby every overpayment is made towards the loan with the highest interest rate with the highest balance. This is a good method, it is easy to remember and relatively efficient, but in general it is not the most efficient. The derivation that follows is based on an ideal model, which does away with the discrete nature of actual loans. In order to find the most efficient payment, a more computationally expensive search in the payment set should be preformed. I came up with an iterative algorithm¹ which came close to the payments prescribed by this model, but I wasn't sure how to prove its efficiency.

The method is not too difficult, requiring no more than a first year course of Calculus to fully understand the mathematics involved.

Suppose you have a loan with initial principal \(P\), interest rate \(r\) over some period², and payment \(\$\) that begins the next period. We find the principal at period \(n\) to be $$\begin{aligned} P_{1} &= Pr - \$\\\\ P_{2} &= P_{1}r - \$\\ &= (Pr - \$)r - \$\\ &= Pr^{2} - \$r - \$\\\\ P_{3} &= Pr^{3} - \$r^{2} - \$r - \$\\ &\ldots\\ P_{n} &= Pr^{n} - \$r^{n-1} - \ldots - \$r - \$\\ &= Pr^{n} - \$\sum_{l=0}^{n-1}r^{l}. \end{aligned}$$

That geometric series can be written another way³, giving us $$P_{n} = Pr^{n} - \$\frac{1 - r^{n}}{1 - r}.$$

If \(P_{n} = 0\) the loan is paid off. So we solve for \(n\) $$\begin{aligned} 0 &= Pr^{n} - \$\frac{1 - r^{n}}{1 - r}\\ \$\frac{1 - r^{n}}{1 - r} &= Pr^{n}\\ \$\frac{r^{-n} - 1}{1 - r} &= P\\ r^{-n} - 1 &= \frac{P(1 - r)}{\$}\\ r^{-n} &= \frac{P(1 - r) + \$}{\$}\\ n &= -\log_{r}\bigg(\frac{P(1 - r) + \$}{\$}\bigg).\\ \end{aligned}$$

\(\$n\) is the total amount paid for the loan, \(\$n - P\) is the total interest paid. We can see \(n\) as a function and write $$n[P,r,\$] = -\log_{r}\bigg(\frac{P(1 - r)}{\$} + 1\bigg).$$

Now suppose we have a one-time overpayment \(b\). By paying early, our total payment is
\(\$n[P-b,r,\$] + b\). This reads "the monthly payment times the number of monthly payments you make when the principal is \(P - b\), plus the \(b\)." If you want to find how much interest you save by making this payment, you subtract this from the total amount paid if the principal is \(P\), giving $$\begin{aligned} q[b] &= \$n[P,r,\$] - \$n[P-b,r,\$] - b\\ &= -\$\log_r\bigg(\frac{P(1 - r) + \$}{\$}\bigg) + \$\log_r\bigg(\frac{(P-b)(1 - r) + \$}{\$}\bigg) - b\\ &= \$\log_r\bigg(\frac{(P-b)(1 - r) + \$}{P(1 - r) + \$}\bigg) - b\\ &= \$\log_r\bigg(\frac{P(1 - r) + \$ - b(1-r)}{P(1 - r) + \$}\bigg) - b\\ &= \$\log_r\bigg(1 - \frac{b}{P + \frac{\$}{1-r}}\bigg) - b \end{aligned}$$

Now, suppose we have several loans, and we want to know how we should use our overpayment to full effect. We want every increment of overpayment to go to the loan with the highest rate of savings. The incremental rate of savings is the derivative of our savings function, found to be $$\begin{aligned} \frac{d}{db}q &= \frac{d}{db}\$\log_{r}\bigg(1 - \frac{b}{P + \frac{\$}{1-r}}\bigg) - \frac{db}{db}\\ &= \frac{\$}{\log r}\frac{d}{db}\log\bigg(1 - \frac{b}{P + \frac{\$}{1-r}}\bigg) - 1\\ &= \frac{\$}{\log r}\frac{\frac{d}{db}\big(1 - \frac{b}{P + \frac{\$}{1-r}}\big)}{\big(1 - \frac{b}{P + \frac{\$}{1-r}}\big)} - 1\\ &= \frac{\$}{\log r}\frac{-\big(P + \frac{\$}{1-r}\big)^{-1}}{1 - b\big(P + \frac{\$}{1-r}\big)^{-1}} - 1\\\\ q' &= \frac{1}{\frac{\log r}{\$}\bigg(b - \big(P + \frac{\$}{1-r}\big)\bigg)} - 1. \end{aligned}$$

For multiple loans we shall use a subscript \(q'_{i}[b]\) to denote the variables associated with each loan, writing $$ q'_{i}[b] = \frac{1}{A_{i}b + C_{i}} -1 \qquad where,\\ A_{i} = \frac{\log r_{i}}{\$_{i}} \qquad and \qquad C_{i} = -\frac{\log r_{i}}{\$_{i}}\bigg(P_{i} + \frac{\$_{i}}{1-r_{i}}\bigg). $$

If we have two loans, we will start by paying whichever has the higher initial rate of savings \(q'_{i}[0]\). We will begin to pay the second loan when the incremental rate of savings of the first loan is equal to the initial rate of savings on the second loan. Sketching it out on a graph, it's like we ski down the first slope until we are level with the second slope's intersection with the axis, then we ski down both of them simultaneously.

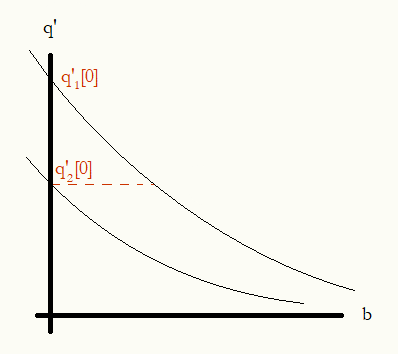
To find it exactly we will need the inverse function of our rate of savings function \(Q = q'^{-1}\), given $$\begin{aligned} B &= \frac{1}{Ab + C} - 1\\ A(B+1)b + C(B+1) &= 1\\ A(B+1)b &= 1 - C(B+1)\\ b &= \frac{1 - C(B+1)}{A(B+1)}\\\\ Q_{i}[B] &= \frac{1 - C_{i}(B+1)}{A_{i}(B+1)}. \end{aligned}$$

Thus we begin to pay overpayment to the second loan at \(Q_1[q'_{2}[0]]\). Generalizing this to \(m\) loans, we first order the loans so that \(q'_{1}[0] < q'_{2}[0] < \cdots < q'_{m}[0]\). Then we create a sequence \(\beta_i\) that defines when to start paying each consecutive loan. We already know \(\beta_1 = Q_1[q'_2[0]]\). $$\begin{aligned} \beta_1 &= Q_1[q'_ 2 [0]]\\ \beta_2 &= Q_1[q'_ 3 [0]] + Q_2[q'_ 3 [0]]\\ &\cdots\\ \beta_i &= \sum_{j = 1}^{i} Q_j[q'_ {i+1} [0]] \end{aligned}$$

Knowing our overpayment \(b\) and taking \(\beta_0 = 0\), we pay \(b\) against \(i\) loans when \(\beta_{i-1} < b \leq \beta_i\). Remember that our loans are ordered by initial rate of savings, and we will pay the first \(i\) loans and no more. If we did not remember this, our algorithm would try to pay negative values. As much as we would like this, it is sadly impossible.

Now that we know how many loans to pay our overpayment against, we will set our overpayment equal to the sum of our inverse rate-of-savings function \(b = \sum Q_j\). We will then invert this sum of inverses⁴ to give us the rate of savings we end up at, which is $$\begin{aligned} b &= \sum_{j=1}^{i}\frac{1 - C_{j}(B+1)}{A_{j}(B+1)}\\ b &= \sum\frac{1}{A_{j}(B+1)} - \sum\frac{C_{j}}{A_{j}}\\ b + \sum\frac{C_{j}}{A_{j}} &= \frac{1}{(B+1)}\sum\frac{1}{A_{j}}\\\\ B^* &= \frac{\sum\frac{1}{A_{j}}}{b + \sum\frac{C_{j}}{A_{j}}} - 1. \end{aligned}$$

We plug this value into our individual inverse functions to know how much we will pay against each loan to achieve the maximum savings. \(b = \sum b_j\) where \(b_j = Q_j[B^*]\).

If we want, we can also take these amounts and apply them to our savings function to find out what the maximum savings actually was \(q^* = \sum q_j[Q_j[B^*]]\).